There’s a long-standing debate about if and how parental socioeconomic status moderates the heritability of IQ. Research has often but not always found that heritability is lower in low-SES families. See Turkheimer and Horn’s excellent review for details (although some of Turkheimer’s own research on this is less than convincing).
Robert Kirkpatrick and colleagues have conducted what may be the best study on the question so far. They use a big Minnesota sample, comprising about about 2500 pairs of adolescent twins, non-twin biological siblings, and adoptive siblings, and investigate if SES moderates either genetic or environmental determinants of IQ.
Below are two graphs showing their main results, demonstrating how SES, measured as a composite of parental educational attainment, parental occupational status, and household income, influences the ACE variance components in the adolescent Minnesota sample. SES increases from left to right, and the values on the x-axis indicate the cumulative proportions of families at or below each SES level. The ACE components are additive heredity (A), shared or common family environment (C), and non-shared or individual-specific environment (E).
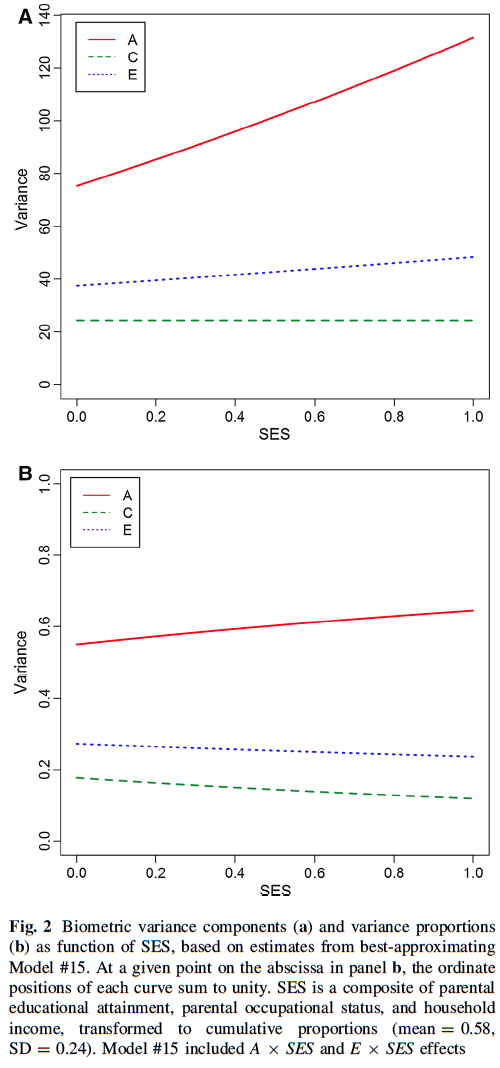
The top graph shows the unstandardized values of ACE components, based on the original IQ metric. Eyeballing the graph, the total unstandardized phenotypic variance appears to be about 140 in the lowest-SES families, while it’s about 200 in the highest-SES families. Taking square roots of these values, we get 11.8 and 14.1. These are the standard deviations of IQ, in IQ points, at the two extremes of the SES variable. This difference is mainly caused by the fact that genetic variance is about 75 at the lowest SES level while it’s about 130 at the highest SES level. The contributions of shared and unshared environmental variances are similar across SES levels. The results show that SES does moderate the heritability of IQ in this sample, albeit not very strongly — genes are more important than environment even in the most deprived family environments.
The bottom graph shows the same results but on a standardized metric where IQ variance is constrained to 1.0 across SES levels. The standardized genetic variance, or heritability, is about 55 percent at the lowest values of the SES variable, and a bit more than 60 percent at the top SES level, with the environmental variances following a corresponding but opposite pattern. Given that the total variance on the original IQ metric increases with SES, the unstandardized values are perhaps more interpretable.
What does it mean when heritability is lower at lower SES levels? One way to think about it is that impoverished environments prevent the realization of genetic potential. Somewhat perplexingly, Kirkpatrick et al. however found that heritability did not change as a function of trait level — i.e., dullness and smartness were equally due to genetic differences. Paradoxically, based on these results, it could also be argued that an individual’s genetic liability towards both high and low intelligence is less likely to be expressed in poor and uneducated families.
There are some other interesting results in the paper. For example, using the adoptee sample they were able to estimate the main effect of SES on IQ. The placement of an adoptee in a family with the lowest SES versus the very highest SES was associated with a 7 IQ point difference. While a causal interpretation of this effect depends on the untested assumption of random placement of adoptees in families, the magnitude sounds plausible to me.
What I think would facilitate the interpretation of SES-heritability interactions would be the use of latent factor models to conceptualize cognitive ability in these studies. When intelligence is defined as a single IQ score, as in Kirkpatrick’s study, it’s difficult to understand how any moderating effects actually operate. With a factor model of IQ, it would be possible examine if the same model applies throughout the SES range, that is, do SES differences cause differences in latent abilities, or is SES moderation actually due to the testing instrument “breaking down” at lower SES levels.
References
Kirkpatrick, R.M., et al. (2015). Replication of a Gene–Environment Interaction Via Multimodel Inference: Additive-Genetic Variance in Adolescents’ General Cognitive Ability Increases with Family-of-Origin Socioeconomic Status. Behav Genet., 45, 200-14.
Discover more from Human Varieties
Subscribe to get the latest posts sent to your email.

The fundamental problem with this kind of research is that “SES” is not some random completely exogenous variable. It too is a function of A. Looking for modulation by SES is essentially removing some of the heritable variance from the analysis. Any such results are bound to be junk accordingly.
As well, they tested children. IQ is known to be unreliable (C doesn’t completely go away) before adulthood. That explains the findings from the adopted sample.
And let’s not forget our old friend measurement error. I wouldn’t be surprised if there’s systematic variation in error by SES.
Kirkpatrick et al. are well aware of the passive gene-environment correlation between SES and IQ genes. According to Purcell’s simulations, the model used produces unbiased estimates of G×SES even when there’s a genetic correlation between the two. This is because the main effect of SES on IQ is modeled, which means that the genetic analysis is actually done on the part of IQ variance that is independent of SES.
Even if there were differences in measurement error by SES level, how would this compromise the moderator analysis?
@Dalliard:
I’m not sure that’s kosher, though.
In any case, we are still talking about children. A study that produced such an effect in adults would be more convincing.
@Dalliard:
Measurement error that systematically varies by IQ could easily produce a spurious GxE effect.
For the record, I’m fairly certain the whole idea of GxE is bogus.
Your IQ as a teenager is pretty important for your future, regardless of its determinants.
I thought you meant measurement error in the SES variable. I agree that IQ measurement bias could produce a G×SES effect. That’s why I think a measurement model for IQ should be used in this research.
@Dalliard:
The part that’s important to your future may not be the part that appears modulated by SES, if you’re feeling me. 😉
That is really bizarre. When people talk about lower heritability for lower SES, it seems to me that they always talk about equal A, but variable C (negative slope), since heritability is a proportion. In fact, any such trend in A is necessarily C from the perspective the whole population, yet we don’t see much C when we look at the whole population.
I’m not sure I understand your point, but generally the standardized ACE values are difficult to interpret when there’s G×SES. You should look at the variances on the raw metric instead.
However, Kirkpatrick et al. point out that the lack of C×SES may be artefactual in their analysis. This is because the inclusion of SES main effects in the model partials out some C variance, possibly rendering C×SES effects impossible.
@Douglas Knight:
That’s a great point. If there’s no C variance in the whole population there should be none in subpopulations.