My defense of psychometric g has attracted more attention than I expected. It has been discussed on Metafilter, Noahpinion, Less Wrong, and iSteve, among other places. In this post, I will address some criticisms of my arguments and comment on a couple of issues I did not discuss earlier.
1. What did Cosma Shalizi claim about the positive manifold?
I wrote that according to Shalizi, the positive manifold is an artifact of test construction and that full scale scores from different IQ batteries correlate only because they are designed to do that. This has been criticized as misrepresenting Shalizi’s argument. I based my interpretation of his position on the following passages, also quoted in my original post:
The correlations among the components in an intelligence test, and between tests themselves, are all positive, because that’s how we design tests. […] So making up tests so that they’re positively correlated and discovering they have a dominant factor is just like putting together a list of big square numbers and discovering that none of them is prime — it’s necessary side-effect of the construction, nothing more.
[…]
What psychologists sometimes call the “positive manifold” condition is enough, in and of itself, to guarantee that there will appear to be a general factor. Since intelligence tests are made to correlate with each other, it follows trivially that there must appear to be a general factor of intelligence. This is true whether or not there really is a single variable which explains test scores or not.
[…]
By this point, I’d guess it’s impossible for something to become accepted as an “intelligence test” if it doesn’t correlate well with the Weschler [sic] and its kin, no matter how much intelligence, in the ordinary sense, it requires, but, as we saw with the first simulated factor analysis example, that makes it inevitable that the leading factor fits well.
It is true that Shalizi does not explicitly claim that it would be possible to construct intelligence tests that do not show the usual pattern of positive correlations. However, he does assert, repeatedly, that the reason that the correlations are positive is because that’s the way intelligence tests are designed. I don’t think it’s an uncharitable interpretation to infer that Shalizi thinks that a different approach towards designing intelligence tests would produce tests that are not always positively correlated. Why else would he compare test construction to “putting together a list of big square numbers and discovering that none of them is prime”?
Another issue is that it can never be inductively proven that all cognitive tests are correlated. However, intelligence testing has been around for more than 100 years, and if there were tests of important cognitive abilities that are independent of others, they would surely have been discovered by now. Correlations with Wechsler’s tests or the like is not how test makers decide which tests reflect intelligence. There’s a long history of attempts to go beyond the general intelligence paradigm.
2. Can random numbers generate the appearance of g?
Steve Hsu noted that people who approvingly cite Shalizi’s article tend to not actually understand it. A big source of confusion is Shalizi’s simulation experiment where he shows that if hypothetical tests draw, in a particular manner, on abilities that are based on randomly generated numbers, the tests will be positively correlated. This has led some to think that factor analysis, the method used by intelligence researchers, will generate the appearance of a general factor from any random data. This is not the case, and Shalizi makes no such claim. The correlations in his simulation result from the fact that different tests tap into some of the same abilities, thus sharing sources of variance. If the randomly generated abilities were not shared between tests, there’d be no positive manifold.
3. What I mean by “sampling”
Several commenters have thought that when I wrote about the sampling model, I was referring specifically to Thomson’s original model which is the basis for Shalizi’s simulation experiment. This is not what I meant. It’s clear that Thomson’s model as such is not a plausible description of how intelligence works, and Shalizi does not present it as one. I should have been more explicit that I regard sampling as a broad class of different models that are similar only in positing that many different, possibly uncorrelated neural elements acting together can cause tests to be correlated. Shalizi argues that evolutionary considerations and neuroscience findings favor sampling as an explanation of g. My argument is that none of this falsifies general intelligence as a trait.
4. Race and g
Previously, I did not discuss racial differences in g, because that issue is largely orthogonal to the question of whether g is a coherent trait. Arthur Jensen argued that the black-white test score gap in America is due to g differences, but the existence of the gap is not contingent on what causes it. James Flynn pointed this out when criticizing Stephen Jay Gould’s book The Mismeasure of Man:
Gould’s book evades all of Jensen’s best arguments for a genetic component in the black-white IQ gap, by positing that they are dependent on the concept of g as a general intelligence factor. Therefore, Gould believes that if he can discredit g, no more need be said. This is manifestly false. Jensen’s arguments would bite no matter whether blacks suffered from a score deficit on one or 10 or 100 factors.
Regarding whether group differences in IQ reflect real ability differences, Shalizi has the following to say:
The question is whether the index measures the trait the same way in the two groups. What people have gone to great lengths to establish is that IQ predicts other variables the same way for the two groups, i.e., that when you plug it into regressions you get the same coefficients. This is not the same thing, but it does have a bearing on the question of measurement bias: it provides strong reason to think it exists. As Roger Millsap and co-authors have shown in a series of papers going back to the early 1990s […] if there really is a difference on the unobserved trait between groups, and the test has no measurement bias, then the predictive regression coefficients should, generally, be different. [15] Despite the argument being demonstrably wrong, however, people keep pointing to the lack of predictive bias as a sign that the tests have no measurement bias. (This is just one of the demonstrable errors in the 1996 APA report on intelligence occasioned by The Bell Curve.)
Firstly, the APA report does not claim that a lack of predictive bias suggests that there’s no measurement bias. The report simply states that as predictors of performance, IQ tests are not biased, at least not against underrepresented minorities. This is important because a primary purpose of standardized tests is to predict performance.
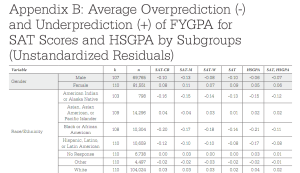
Secondly, research does actually show that the performance of lower-IQ groups is often overpredicted by IQ tests and other g-loaded tests, something which is alluded to in the APA report as well. This means that the best-fitting prediction equation is not the same for all groups. For example, the following chart (from this paper) shows how SAT scores (and high school GPA) over- or underpredict first-year college GPA for different groups:
There’s consistent overprediction for blacks, Hispanics, and native Americans compared to whites and Asians. Female performance is underpredicted compared to males, which I’d suggest is largely due to sex differences in personality traits.
As another example, here are some results from a new study that investigated predictive bias in the Medical College Admission Test (MCAT):
Again, the performance of blacks and Hispanics is systematically overpredicted by the MCAT. Blacks and Hispanics are less likely to graduate in time and to pass a medical licensure exam than whites with similar MCAT scores.
But as noted by Shalizi, the question of predictive bias is separate from the question of whether a test measures the same thing across groups. These days, psychometricians maintain that to establish that the same traits are being measured in different groups there must be an analysis of what is called measurement invariance. Several studies have investigated this question with respect to the black-white IQ gap, and they affirm that the gap can generally be regarded as reflecting genuine differences in the latent traits measured (Dolan 2000; Dolan & Hamaker 2001; Lubke et al. 2003; Edwards & Oakland 2006).
In contrast, analyses of test score gaps between generations (or the Flynn effect) indicate that score gains by younger cohorts cannot be used to support the view that intelligence is genuinely increasing (Wicherts et al. 2004; Must et al. 2009; Wai & Putallaz 2011). Measurement invariance generally holds for black-white differences but not for cohort differences. Wicherts et al. 2004 put it this way:
It appears therefore that the nature of the Flynn effect is qualitatively different from the nature of B–W [black-white] differences in the United States. Each comparison of groups should be investigated separately. IQ gaps between cohorts do not teach us anything about IQ gaps between contemporary groups, except that each IQ gap should not be confused with real (i.e., latent) differences in intelligence. Only after a proper analysis of measurement invariance of these IQ gaps is conducted can anything be concluded concerning true differences between groups.


Shalizi has entirely sworn off this topic altogether, long ago (so, in particular, @noahsmith’s hopeful twitter is likely not to be answered).
His most recent comments on the topic seem to be in his Advanced Data Analysis notes, freely available in this PDF:
http://www.stat.cmu.edu/~cshalizi/ADAfaEPoV/ADAfaEPoV.pdf
Your post was also mentioned on Steve Hsu’s blog.
http://infoproc.blogspot.co.nz/2013/04/myths-sisyphus-and-g.html
Kiwiguy,
Dalliard links to Hsu’s post in the first sentence of Part 2.
Cheers Pincher. The comments on Metafilter make for frustrating reading. So pious and condescending.
My defence of Shalizi, which is growing rather long and is two long to cross post here as a comment, I have made available here:
http://previousdissent.com/forums/showthread.php?23562-What-if-anything-does-Cosma-Shalizi-mean-by-g-is-a-myth
‘What, if anything, does Cosma Shalizi mean by “g is a myth”‘
A fraction distilling the main point: Proceeding then to the defence of Cosma Shalizi’s post:
Here is how he summarises the whole post — what he intends to say (though one can quibble with the execution):
‘To summarize what follows below (“shorter sloth”, as it were), the case for g rests on a statistical technique, factor analysis, which works solely on correlations between tests. Factor analysis is handy for summarizing data, but can’t tell us where the correlations came from; it always says that there is a general factor whenever there are only positive correlations. The appearance of g is a trivial reflection of that correlation structure. A clear example, known since 1916, shows that factor analysis can give the appearance of a general factor when there are actually many thousands of completely independent and equally strong causes at work. Heritability doesn’t distinguish these alternatives either. Exploratory factor analysis being no good at discovering causal structure, it provides no support for the reality of g.
Every sentence of that paragraph is true as written, except possibily the one related to heritability — a topic Dalliard has reservations about, but is not willing to discuss at this time to explain what they are, although I have asked him to. There is an important reservation to the statement about ‘1916’ [which is Thompson’s sampling model, clearly, in reference to Spearman’s ‘two factor’ model (one general, g, and one specific per subtest (mental faculty)], which Glymour would surely know and Shalizi probably does as well, and which I shall mention later.’
…
If Dalliard is going to win against logic and mathematics, it is entirely on the strength of refuting the once sentence in the next paragraph, ‘Since that’s about the only case which anyone does advance for g,’ The way is open there, because it has to do about the literature, not mathematics or the logic of causal inference — and not in relation to explanation vs. description, that is causal reasoning vs. associative, ‘statistical’, reasoning.
…
Dalliard would do well to elaborate his #2 as an attack, and to flesh out his claims about heritability so we may all examine what, if anything, Dalliard can make stick.
It is clear to me that none of the commentators so far have gotten to the essence of the argument, which is about causation. Read Shalizi’s post again. Does he mention causation? Do his critics make it central to their argument or mention it at all? To the extent that they do not, they are indulging in the fallacy ignoratio elenchi — a refusal to engage the argument at all. Those who do not reason from causal diagrams, after the manner of Pearl and Glymour, nor comment upon them, have not engaged the argument.
…
As far as what Shalizi thinks ‘the myth of g’ is, he tells us himself in his conclusion:
‘Building factors from correlations is fine as data reduction, but deeply unsuited to finding causal structures. The mythical aspect of g isn’t that it can be defined, or, having been defined, that it describes a lot of the correlations on intelligence tests; the myth is that this tells us anything more than that those tests are positively correlated.’
Are the positive correlations of the tests, even when we try very hard to negate those correlations, proof of causal inference demonstrating the existence of g? No. According to Pearl (and Glymour) observation alone — even vastly constrained observation, cannot generate a causal inference. To argue otherwise, in the teeth of Pearl and Glymour, and to attack Shalizi on the strength of an argument that ignores his main point, is sophistry. This statement is true, as a matter of causal logic (as we have come to understand it in the last 20 years or so) — even if the world is so constituted that we can *never* violate the positive manifold condition, in any practical testing situation.
Here is a crazy idea Macrobius. Let us not waste our time arguing these old points. If you think you have a better way to analyze intelligence test data and important outcomes that determine causality then do it. Download some data and make a few DAGs or whatever and school us.
The purpose of factor analysis is to come up with potential causal variables. Whether those variables correspond to anything interesting must be established based on evidence that is extrinsic to factor analysis. No one argues that factor analysis alone can prove that g is a real and important human trait. This is why I described at length those other lines of evidence in my original post. Shalizi ignores all such inconvenient findings and attacks the straw man that the positive manifold and the results of exploratory factor analysis are “the only case which anyone [advances] for g”. The results are predictably uninformative.
This has been explained to you several times, so this is the last time. If it really was that only some subset of all cognitive tests were positively correlated and the consistent finding of positive correlations resulted from test makers’ insistence on using only that subset of tests, then it would be easy to falsify g in every possible sense. However, this is not the case, so Shalizi’s repeated assertions about how tests are constructed to be correlated are simply bogus.
What the positive correlations prove is that there is an explanandum. Something must explain the consistent emergence of the general factor. Whether g is caused by some unitary feature of the brain or by “sampling”, whether and how it is associated with interesting social and biological variables, whether it is invariant across different testing methods, etc. can only be answered using methods other than EFA. The reality or lack thereof of general intelligence is dependent on the results of these different lines of research, which Shalizi ignores.
“The appearance of g is a trivial reflection of that correlation structure. A clear example, known since 1916, shows that factor analysis can give the appearance of a general factor when there are actually many thousands of completely independent and equally strong causes at work. Heritability doesn’t distinguish these alternatives either.”
One problem seems to be that we are conceptualizing “a general factor” differently. I would call the “general factor” extracted from a positive manifold by factor analysis to be “a general factor”. It seems that you make a distinction between the extracted general factor and something else. What this something else is is not clear. And then you go onto argue that g isn’t that something else and so is just an illusion. Cosma Shalizi was clearly off base when he stated or implied or insinuated that the positive manifold was an artifact of test construction. It isn’t and it is something that needs to be explained. If we can’t agree on this point, then further discussion is impossible. The question then is what causes the positive manifold and therefore the extracted general factor by which we mean the general factor extracted from the manifold and not necessarily the something else you mean. We are then concerned with the theory — or model — of general intelligence. Which is the theory of why there is a positive manifold. As to this, we need to look at other evidence. Contrary to your claim the correlation between heritability and g-loadings is one such piece of evidence because it is a non-tautology and so is something that needs to be explained and can not be explained equally well by all theories of g. Another, and related, piece of evidence is the finding of a strong genetic g. See, for example: Shikishima, et al., (2009). Is g an entity? A Japanese twin study using syllogisms and intelligence tests. Other pieces of evidence are the physiological correlates of g. See, for example: Lee, et al. (2012). A smarter brain is associated with stronger neural interaction in healthy young females: A resting EEG coherence study. Intelligence. So there are a lot of pieces of evidence which point to which models are unlikely.
I’m afraid we probably have reached the end of argumentation here, since we are left with asserting contrary premises from which to start — not that it hasn’t been illuminating, to me at least, but we do seem to have reached an impasse. Since if neither the starting premises nor the mode of deduction can be agreed on (and causal inference is new, so it doesn’t have the status of the propositional calculus or first order predicate logic, *even though it claims such primary status* and Shalizi believes in it and uses it), no dialectic may proceed.
‘This has been explained to you several times, so this is the last time. If it really was that only some subset of all cognitive tests were positively correlated and the consistent finding of positive correlations resulted from test makers’ insistence on using only that subset of tests, then it would be easy to falsify g in every possible sense. However, this is not the case, so Shalizi’s repeated assertions about how tests are constructed to be correlated are simply bogus.
‘What the positive correlations prove is that there is an explanandum. Something must explain the consistent emergence of the general factor. Whether g is caused by some unitary feature of the brain or by “sampling”, whether and how it is associated with interesting social and biological variables, whether it is invariant across different testing methods, etc. can only be answered using methods other than EFA. The reality or lack thereof of general intelligence is dependent on the results of these different lines of research, which Shalizi ignores.’
Again, I will re-iterated my assertion that nothing rides on whether tests may be constructed or not in that fashion, nor on Shalizi’s beliefs about the matter. That is because even if the *observational* data (absent an experimental intervention or a causal inference approved by Glymour’s Tetrad II program and analysis of DAGs) were such that some r=1.0 correlation were observed, it would *still* not suffice, to Glymour, Pearl, and Shalizi. This is because there is (on their view) a radical and unbridgeable difference between description and explaining. To assert that observations can result in an [i]explicandum[/i] is simply to reject the premise on which the argument is being made, and thus has no logical force against it. It means you have a radical disagreement with Shalizi, prior to engaging his deductions at all.
So, johnfuerst’s comment is correct. No one disputes that g can emerge in the context of descriptive, *associational* statistics. The bone of contention is whether it can or has crossed the bridge of death to the explanatory world of causation.
Now, you can call this point of view of Shalizi and other AI researchers idiotic, sterile, or criticise it as a possible basis for future Social Science from any number of perspectives — but you still have not engaged Shalizi’s post if you do not accept his view of the matter as to what constitutes proper logical reasoning and mathematics — and these questions are entirely prior (in a philosophical sense) to even Science and its concerns.
Shalizi’s critique, for example, applies equally to Noah Smith’s hope that Japanese monetary policy will be a Natural Experiment — because by this logical critique and philosophical theory of causation, *all* Natural Experiments in economics based solely on observation are fatally flawed and do not yield explanatory (vs. descriptive) conclusions.
I don’t claim to have done more than to point out to you the centrality of this aspect of Shalizi’s reasoning — and not least in the post he made. It’s not obvious, and needs highlighting. In his latest version of his Advanced Data Analysis by Elementary Methods course, which I linked previously, he devotes a whole section (‘Part III’) to causal inferences, as does the Glymour 1998 paper and Pearl’s work, all referenced in Shalizi’s post. Oddly, even though Part II is practically a recap of his post, Part III mentions it less even than the work of Glymour. I’ve pointed out one reason that may be — that if you take his theory of causal inference seriously, you must realise that his sampling model violates one of the two central qualities models usually have, if they are not exceptional in causal inference, namely the markov property and faithfulness — specifically linear faithfulness. Glymour does not use Thomson as a bludgeon, even in his contentious 1998 article. Shalizi does. There, I think, you might concentrate your forces and win. But only if you wish to *engage*.
Will this lead to some new result in Psychometrics? I doubt it. It is an intensely destructive observation Shalizi has made. He has a neutron bomb to sterilise all of Social Science, and he chooses to go after one pet peeve of his. It is as sterile as pointing out that Euler used an incoherent notion of the infinitesimal to do Calculus, and would flunk any modern Real Analysis course — but that is not to say that epsilons and their deltas and the notion of a limit were fruitless, or that some justification for Euler’s intuitions would two centuries later be found (by A. Robinson in 1962, with non-standard analysis).
My claim is simply that in your current line of attack at this blog, you haven’t engaged him. You may have any number of reasons for refusing to do so — but refusing to engage and argument, and simulating a refutation of it, is a sophistical and fallacious proceeding, and unworthy of Science.
Yes, this isn’t going anywhere. My argument is that Shalizi ignores all the best evidence that has been presented in support of general intelligence (including evidence from studies using his favored “causal” methods) and makes many factually false assertions in order to bolster his case. You argue that this has no bearing on the validity of his case against g.
He also writes:
Had Shalizi considered the full case for g, would he have ended up thinking that g has “some claim on us” because alternative theories aren’t tenable? We don’t know that. But what’s clear is that had he honestly grappled with the totality of evidence, his article would have been very different and would probably not have attained a reputation as the definitive refutation of g.
One caveat about his ‘favoured causal methods’ is that CFA is necessary, but not sufficient, as a causal explanation at larger sample sizes. It has an 80% rate of false negatives (beta, low power).
Econometrics and epidemiology seem to have embraced DAG testing to some extent (the former field ad hoc), and psychometrics not yet. There really is no substitute for writing down your causal model in graphical form or some other. Until that is done in psychometrics, I really don’t see a chance for a conversation with Shalizi:
‘The ideas people work with in areas like psychology or economics, are really quite tentative, but they are ideas about the causal structure of parts of the world, and so graphical models are implicit in them.’ (p. 455, http://www.stat.cmu.edu/~cshalizi/ADAfaEPoV/ADAfaEPoV.pdf), as revised 19 days ago.
I think you and I agree his article is not a definitive refutation of g — most of his reliance on ‘causal inference using DAGs’ is not developed, and neither is it familiar to his intended audience. Until we live in a counterfactual world where DAGs are commonly understood to be as important for scientific inquiry as ‘logic itself’, his real argument must remain obscure to his readers.
I think Macrobius is demanding that psychometrics provide an explanation of how g-factor causes the positive manifold in some more robust sense, similar to the one explaining why H2O causally determines the physical identity of water, as if there must be some kind of necessary physical relationship between the explanans and explanandum. But g is a matter of contingency, like anything else in science; some branches of science enable us to establish stronger contingent causal chains than others, but this is only because of the epistemological limitations of human knowledge; it does not invalidate the causal chain itself, whose inductive truthfulness can only be established by the available evidence; nor is it reasonable to expect one contingent causal chain in one branch of science, which is necessarily weak given epistemological limitations, to do the work of a much stronger causal chain in another branch of science, which does not suffer from the same epistemological limitations because it is not operating at the furthest reaches of human knowledge. Causal relationships must always involve some degree of probability and if there is little or no evidence to the contrary, then this would be sufficient guarantee of its inductive truthfulness.
Thus, given the null hypothesis, it would appear that there exists a causal relationship between g-factor and the positive manifold, which is supported by multiple lines of converging evidence (especially CFA, but also psychoneurological correlates of g and heritability estimates); on the other hand, there is very little or no credible evidence in favour of the null hypothesis. The only credible alternative to g-factor, Gardner’s multiple intelligences, assumes that abilities are not positively correlated, but this has not been demonstrated by the available evidence (because g is a robust, empirically verifiable phenomenon). Therefore, it must be concluded, given the supporting evidence, that there is a high probability that g is the causal mechanism that explains the positive manifold and that statistical g is the result of neural g.
Um. It’s not as if the tests are designed at random to thoroughly and evenly cover some space.
s/at random/in an unbiased manner/Different test makers have different ideas of what count as important cognitive skills, and the fact that after 100+ years of test development the positive manifold stands unfalsified tells us all we need to know. For example, the latent factor of “emotional intelligence” tests has a g loading of 0.80 (MacCann et al.).
“Different” doesn’t mean they cover the whole space of things that could possibly be tested.
Take someone from the top of one career ladder and put them in a career or environment that’s as diametrically unrelated as you can think of. Real skills, not questionnaires by trained academics.
The expectation is not that a high-g individual would have the specific skill set needed in a new job from the outset. Rather, the expectation is that he or she will find it easy to learn the ropes and become a good worker in short order. The predictive validity of g is superior to that of job experience (Schmidt & Hunter 2004).
I guess the way I wrote that sounded like I was confusing learning rate with prior knowledge. I know that $g$ is about learning rate. What I actually meant was, let’s think more widely about the breadth of human endeavours. Using real-world skills as a starting point for thinking about all of the things one could possibly value.
Your example of emotional intelligence still sounds to me like overlap among what researchers value. Remember that ∃ many hurdles to get to the place in life that you are designing intelligence tests. Those hurdles as well as the entropy (many directions one can go in life) are going to make the people designing tests homogeneous in their beliefs about what they should be testing and how.
…to say nothing about how difficult it is to do something original even if you’re trying very hard to do so. (An
[[submitted the last one by accident]] (And by the way, have there been a lot of test makers spending the time to try to find truly different things to measure? To find any kind of variable that won’t correlate with $g$? I’m not talking about Raven’s matrices, which are still trying to measure the same old idea of intelligence, just in a neutral way. I mean that your claim that “100 years of tests is enough” should come with some examples that test makers are really trying to spread out and cover the lay of the psychological landscape. Otherwise it’s 100 years of darts being thrown at the same board; no wonder they didn’t land outside the pub.)
A number of leading psychometricians have been quite hostile to the idea of g, but they nevertheless have been incapable of doing away with the positive manifold. Please read my big g factor post where I review the history of attempts to find uncorrelated cognitive abilities; see this chapter in particular. Thurstone, Guilford, and many others after them have devoted their careers to this endeavor but all of them have failed.
Spearman himself noted that the general factor became less clear for very gifted individuals. Now, people refer to this fact as “range restriction”. However, what clearer argument is there against the biological reality of g, than that it is the most clearly defined for the mentally deficient? The more talented the group of individuals is, the more they differ in their abilities, and the less prominent the “g factor” becomes.
In a sense, the analogy with the car that Shalizi brings up is perfect. The more you lower the maximum price for the cars in your sample, the more all other properties become correlated with the price, and price becomes more and more “g loaded”. There simply is less room for variation, when all that variation is curtailed by a small price tag.
The reason SLODR exists is still controversial but most likely it’s due to the fact that g cannot explain differences in performance among highly intelligent people because there are non-intelligence factors which affect performance and bias the measurement (MI fails at this level). Shalizi’s car analogy was addressed in the original post.